课上老师介绍了6种参数更新算法

梯度下降(gradient descent, GD)

# Vanilla update
x += - learning_rate * dx

梯度的方向是从小往大的，也就是从低处指向高处，我们想minimize loss，就是需要从高处往低处走，也就是向梯度的反方向走，所以加上负的梯度。注意：梯度下降算法一般有三种:(a) Batch gradient descent, (b)Stochastic gradient descent， (c)Mini-batch gradient descent; 第一种是每次将训练集所有的example带入来更新梯度，第二种是每次只取训练集中的一个来更新梯度，第三种是每次取训练集的一部分来更新梯度。目前DNN中训练多采用第三种方法来训练，一般说SGD默认也指的是第三种。
缺点:

容易震荡，如图1所示，当横向梯度和纵向梯度不一样的时候，由于各个方向梯度更新的学习率是一致的，这就会导致，横向梯度更新的慢，下降的慢，但是纵向梯度更新的快，造成震荡。
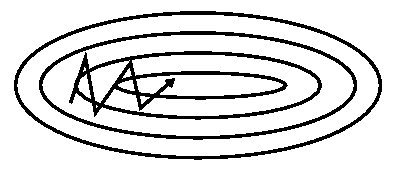
图1： SGD without momentum
不好设学习率，从图一可以看出，当学习率设大的时候，纵向梯度由于较大，就容易跑飞，如果设的较小，由于横向梯度小，要收敛很多次，才能到达极值点。
saddle points的存在，DNN中存在许多saddle points，saddle points的梯度为0,但并不是极值点，所以针对这个缺陷，引入了momentum的方法。

momentum

物理意义上解释就是模拟物体运动的惯性。在SGD中，梯度直接影响位置x，现在是梯度先改变速度v，v来改变位置x。

# Momentum update
v = mu * v - learning_rate * dx # integrate velocity
x += v # integrate position

也可以理解为，每次更新的时候，还会考虑上一次的更新v，mu是一个小于1的系数，一般设为[0.5,0.9,0.95,0.99]中的一个，一般开始设为0.5,随着epoch的增加，提升到0.99。v一般初始化为0.

由于momentum每次更新还会考虑上一次的更新，所以在saddle point的时候，即使梯度为0,但是由于上一次的更新还在，可以帮助我们越过这个saddle point，这就类似与小球从高处滚下来，不会在saddle point处停留。

其次从数学角度考虑，当上一次更新v*mu和这一次的梯度更新- learning_rate * dx一致时，那么更新会增加，就会往前多跑一点，这样会加快收敛;当二者方向不一致，那么会少跑一些，这样会减少震荡。

Nesterov Accelerated Gradient (NAG)

如图2所示:

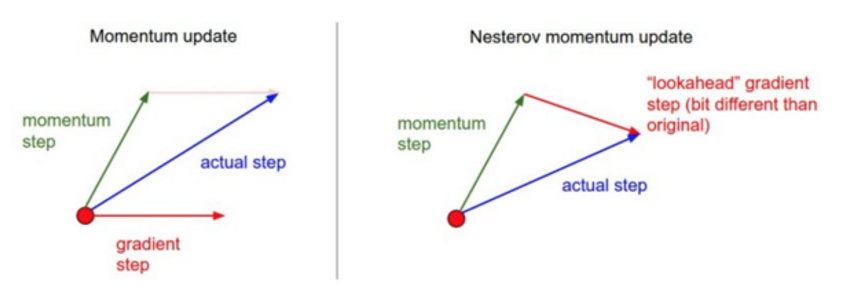
Momentum 算法是考虑上一次的更新和这次的梯度更新，在原点算momentum step 和 gradient step，然后使用向量的累加方式，得到真实的actual step，NAG的想法就是我们肯定是要走momentum step，即x+mu*v,那就走完momentum step，到达新的点后，在新的点求梯度。也就是计算x+mu*v的梯度，而不像是Momentum计算的是x位置的梯度。更简单的理解就是，momentum是先计算当前点x的梯度，在去加mu*v,而NAG是先做x+mu*v,然后计算x+mu*v的梯度来做修正，二者刚好相反。hinton ppt上的图解可以表达这种意思:

x_ahead = x + mu * v
# 计算dx_ahead(在x_ahead处的梯度，而不是在x处的梯度)
v = mu * v - learning_rate * dx_ahead
x += v

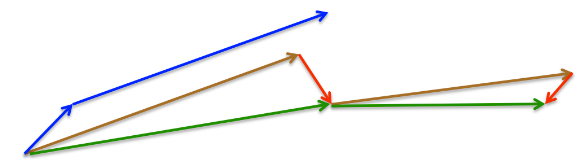
如图3所示:

上面的那段代码，在实践中被人们改写成另外一种方式，通常人们也更喜欢这种方式

v_prev = v # 存储备份
v = mu * v - learning_rate * dx # 速度更新保持不变
x += -mu * v_prev + (1 + mu) * v # 位置更新变了形式

其实这个改写是有公式依据的，第一段代码很容易理解，就是计算x+mu*v的梯度。可以这么说，第一段代码是原始形式的表达，第二段代码是改写形式的表达，公式的推导可以参见知乎专栏比Momentum更快：揭开Nesterov Accelerated Gradient的真面目.该专栏里给出了第二段代码的数学形式: $d_i = \beta d_{i-1} + g(\theta_{i-1}) + \beta [g(\theta_{i-1}) - g(\theta_{i-2})] \tag{1}$ $\theta_i = \theta_{i-1} - \alpha d_i \tag{2}$

公式(1)中可以看出，之所以NAG比momentum快，是因为比momentum多了一项 $g(\theta_{i-1}) - g(\theta_{i-2})$ ,本次梯度想对于上次梯度的变换量，这个变换量的本质就是对目标函数二阶导的近似，因为利用了二阶导信息，所以NAG比momentum有更快的收敛速度。

小结一下，NAG在Momentum的基础上做了点小的改进，比momentum更快。

之前介绍的方法，有一个共同特性，也可以说是缺陷，就是学习率的操作是全局的，对所有参数作用一致，下面介绍一些适应性学习率调参，可以针对不同参数来自适应不同学习率。

Adagrad

# 假设有梯度和参数向量x
cache += dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

cache的维度和dx一致，通过该方法归一化，梯度大的，在除以cache后，会变小，梯度小的，在处以cache后会变大，eps是防止除数为0，一般可以设为1e-5,1e-6,1e-7。平方根操作非常重要，如果去掉，效果会大降。缺点:在深度学习中单调的学习率被证明通常过于激进且过早停止学习。

RMSprop

cache =  decay_rate * cache + (1 - decay_rate) * dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

来源于Hinton 在coursera课程的第六课第29页ppt。通过修改Adagrad方法，通过对梯度平方滑动平均，RMSprop对Adagrad的修改有点类似与momentum对SGD的修改。 decay_rate是一个超参数，常用的值是[0.9,0.99,0.999]。

Adam

m = beta1*m + (1-beta1)*dx  #momentum
v = beta2*v + (1-beta2)*(dx**2)  #RMSprop
x += - learning_rate * m / (np.sqrt(v) + eps)

Adam有点像是momentum和RMSprop的结合，使用平滑的梯度m而不是原来的dx。论文里推荐的参数设置为eps=1e-8, beta1=0.9, beta2=0.999.m和v的初始值设为0. 此外，完整的Adam算法还有一个bias 矫正，代码如下:

m, v = # initialization
for t in xrange(0, big_number):
    dx = # 梯度
    m = beta1*m + (1-beta1)*dx  #momentum
    v = beta2*v + (1-beta2)*(dx**2)  #RMSprop
    m /= 1 - beta1**t
    v /= 1 - beta2**t
    x += - learning_rate * m / (np.sqrt(v) + eps)

小结

learning rate 针对全局的更新算法: SGD --> Momentum --> NAG
learning rate 针对不同参数有所调整的算法：Adagrad --> RMSprop --> Adam
层次关系是依次改进，效果逐渐递增。

推荐使用Adam，或者NAG。

补充

learning rate decay

在训练深度神经网络时，学习率不是一成不变的，会随着epoch的增加，学习率逐渐降低。笔记里给出的理解方式是：学习率开始设置的大，开始系统动能也大，这时候没问题，可以快速收敛，但是收敛到一定程度后，如果学习率依然很大，那么系统动能过大，就有可能越过极值点，导致震荡无法收敛。所以一般的learning rate decay的方法有以下三种:

step decay：每隔多少周期，学习率设为原来的0.1或者多少。经验做法：使用固定学习率来训练，观察验证集错误率，每当错误率停止下降，学习率就乘以一个常数(比如0.5)来降低学习率。
Exponential decay: $\alpha = \alpha_0 e^{-kt}$ ,其中 $\alpha_0, k$ 是超参数，t是迭代次数（也可以是迭代周期数目）
1/t decay: $\alpha = \frac{\alpha_0 }{1+kt}$ ,其中 $\alpha_0, k$ 是超参数，t是迭代次数

二阶方法

二阶方法最常用的是牛顿法 $\theta^* = \theta_0 - H^{-1} \nabla_{\theta}J(\theta_0)$ 需要使用Hessian矩阵，但是不适用于深度神经网络，因为一个深度神经网络参数动辄百万，然后对这个百万的Hessian矩阵求逆，目前的计算机基本不可能。但是优点是没有超参数，如learning rate，可以直接求解，对于一些凸优化问题来说。

参数优化算法