目前激活函数有以下几种：

Sigmoid

$$\sigma(x) = \frac{1}{1 + e^{-x}} \tag{1}$$ 优点如下: 很容易解释神经元的"firing rate",我搜了一下，"firing rate"是神经编码里的名词，具体没有太关注。 缺点如下:

• 容易饱和，导致梯度为0;
• 非zero-centered，即sigmoid的输出的均值为0;
• $exp$操作比较费时，但是相较于卷积这些操作，不足以提之。

注意:非zero-centered指的是sigmoid的输出恒为正，在多层神经网中，sigmoid的输出作为下一级的输入，在反向传播更新参数W的时候，会导致每次更新参数要么全部加，要么全部减，取决与输入。推理如下： $$f=\sum w_ix_i+b \\ \frac{df}{dw_i}=x_i \\ \frac{dL}{dw_i}=\frac{dL}{df}\frac{df}{dw_i}=\frac{dL}{df}x_i$$ 可以看出，由于$x_i$总是大于0(此处$x_i$为这一层的输入，也就是上一层sigmoid的输出)。梯度$\frac{dL}{dw_i}$总是和$\frac{dL}{df}$同号，即要么全为正，要么全为负。这样就会导致zig zag path，至于为什么这么描述，我其实不太理解，不过正常更新参数迭代的时候，在每一轮迭代的过程中，参数$W$中有的增大有的减小，这样可以快速收敛，而不是同时增大或同时减小，这会导致收敛很慢。参考

tanh

$$tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} \tag{2}$$ 缺点:依然容易饱和，导致梯度消失。 不过相对sigmoid来说，解决了zero-centered的问题。

ReLU

$$max(0, x) \tag{3}$$ 优点:

• 不会饱和;
• 计算很快;
• 收敛快(sigmoid/tanh的6倍) 缺点：
• 非zero-centered的输出;
• 当输入为小于0的时候，ReLU输出为0,这就很有可能导致该参数一直无法更新.

注意:由于小于0,被抑制，所以在使用ReLU的时候，通常给bias初始化为0.01。例如，将学习率设为较大的时候，可以发现40%的W一直被抑制。当然一般开始的学习率都会设置的比较合理，不会过大。

Leaky ReLU

$$max(0.1x, x) \tag{4}$$ 优点:

• 不会饱和;
• 计算快;
• 收敛快(sigmoid/tanh的6倍)
• 不会出现ReLU在小于0的时候，就出现抑制的情况。

注意:还有一种PReLU激活函数:$f(x) = max(\alpha x, x)$, $\alpha$作为一个参数放在网络里学习。

Maxout

$$max(w_1^T x + b_1, w_2^T x + b_2) \tag{5}$$ 优点如下:

• ReLU和Leaky ReLU形式的扩展，他们的优点他都有;
• 不会出现抑制的情况; 缺点：
• 激活函数的参数$w_1^T$等变多。

ELU

$$f(x) = \left\{ \begin{array}{rl} &x &if& x > 0\\ &\alpha (e^x - 1) & if& x \leq 0 \end{array} \right. \tag{6}$$ 优点如下:

• ReLU有的优点他都有;
• 不会被抑制;
• 输出的结果接近Zero mean. 缺点:
• $exp$操作耗时。

激活函数图如下图所示:

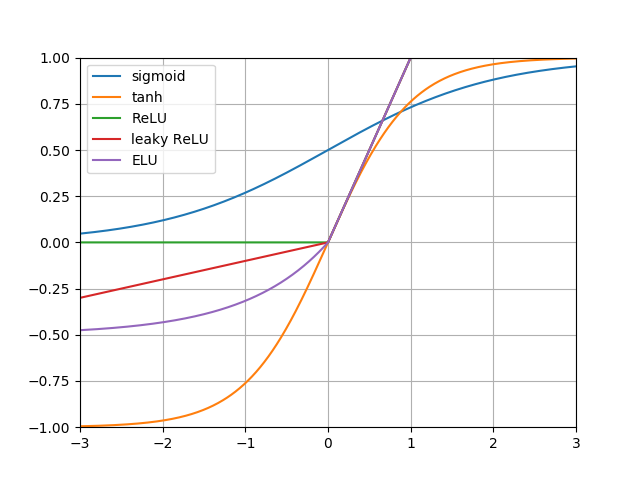
小结

在实际实验中：

• 使用ReLU;
• 可以尝试Leaky ReLU/maxout/ELU
• 不要使用Sigmoid和tanh