课上介绍了两种数据处理方式:

归一化

X -= np.mean(X, axis = 0)  # Mean subtraction
X /= np.std(X, axis = 0)  # Normalization

效果如下图所示:

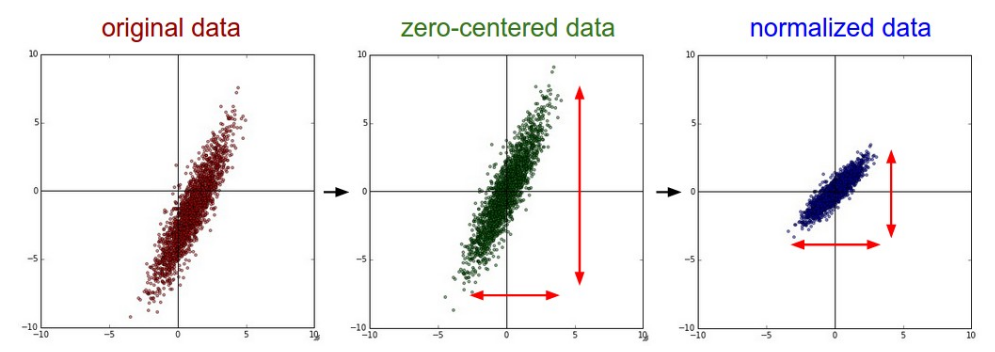
PCA降维和白化

# Assume input data matrix X of size [N x D]
X -= np.mean(X, axis = 0) # zero-center the data (important)
cov = np.dot(X.T, X) / X.shape[0] # get the data covariance matrix

# 使用SVD求解的原因是因为协方差矩阵是对称的，也是半正定的
U,S,V = np.linalg.svd(cov)  # U:eigenvectors，S:1-D array of the singular values

Xrot = np.dot(X, U) # decorrelate the data

# whiten the data:
# divide by the eigenvalues (which are square roots of the singular values)
Xwhite = Xrot / np.sqrt(S + 1e-5)  # 加1e-5是为了防止出现特征值为0

效果如下图所示:

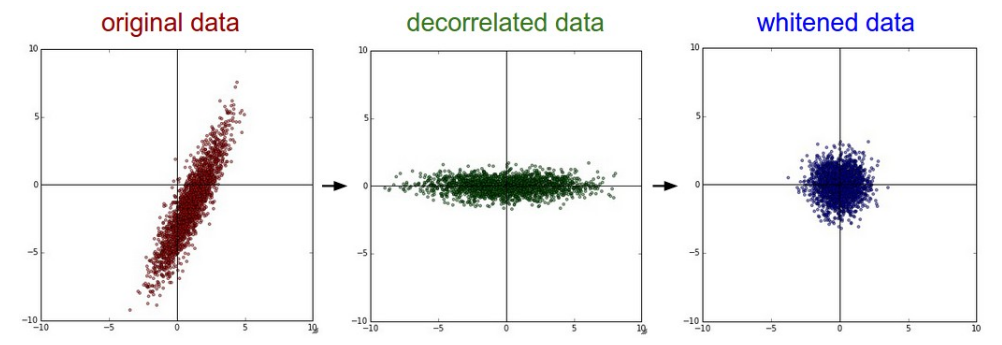
讲义里说白化这个方法可以放大噪声，使其凸显出来，不过我自己写了个代码，发现噪声在做完PCA就你看出来，百化之后稍微明显点，离中心点更远了。

注意：在Mean subtraction操作中，对于真实RGB图像来说，有三个通道，有两种处理方式:

• 直接三通道混合去均值(AlexNet)
• 单独对每个通道做Mean subtraction(VGGNet)